1+x^4=(x^2-√2x+1)(x^2+√2x+1),按有理函数的部分分解的方法,1/(1+x^4)=1/(2√2)×[(x+√2)/(x^2+√2x+1)-(x-√2)/(x^2-√2x+1)],接下来把分子拆成两部分:一部分是分母的导数的一个倍数,一部分是常数,这是有理函数的不定积分的定式.
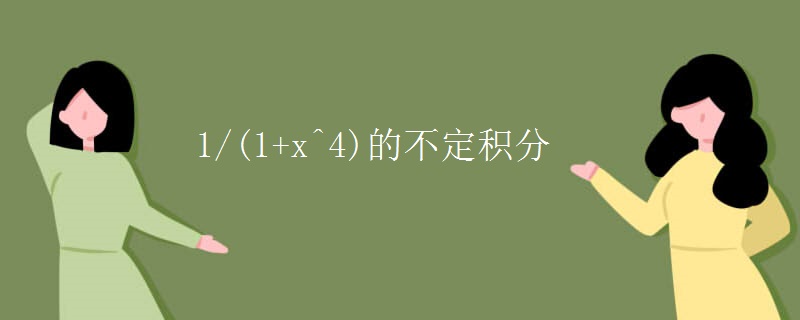
1/(1+x^4)的不定积分怎么算?
∫ dx/[x(1+x⁴)]。
令u=x⁴,du=4x³ dx
原式= ∫ 1/[x*(1+u)] * du/(4x³)
= (1/4)∫ 1/[u(u+1)] du
= (1/4)∫ (u+1-u)/[u(u+1)] du
= (1/4)∫ [1/u - 1/(u+1)] du
= (1/4)(ln|u| - ln|u+1|) + C
= (1/4)ln|x^4| - (1/4)ln|x^4+1| + C
= ln|x| - (1/4)ln(x^4+1) + C
